12 KiB
+++ author = "Wxn" title = "2024-04-20七大排序算法+层序遍历" date = "2024-04-20" description = "Please read me first." tags = [ "Dilay", ] categories = [ "面试复盘", ]
+++
This article offers a sample of basic Markdown.
正文开始
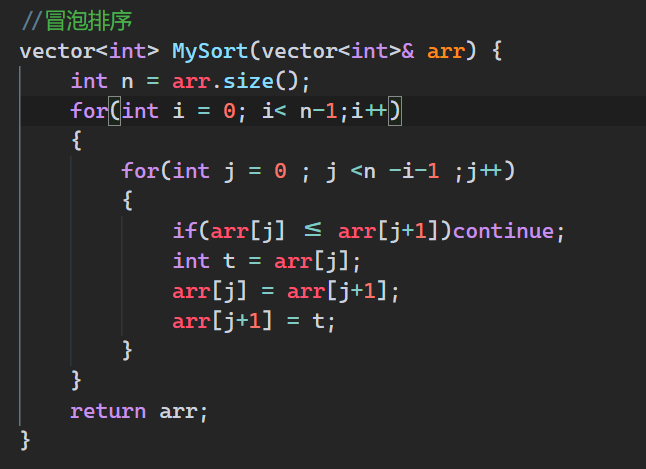
1.冒泡排序(从小到大)
#include <iostream>
#include <vector>
using namespace std;
//冒泡排序
vector<int> MySort(vector<int>& arr) {
int n = arr.size();
for(int i = 0; i< n-1;i++)//冒泡排序和选择排序都是0~n-1轮
{
for(int j = 0 ; j <n -i-1 ;j++)
{
if(arr[j] <= arr[j+1])continue;
int t = arr[j];
arr[j] = arr[j+1];
arr[j+1] = t;
}
}
return arr;
}
int main()
{
vector<int> arr{5,2,3,1,4};
for(auto it : arr)
{
cout<<it<<" ";
}
cout<<" "<<endl;
MySort(arr);
for(auto it : arr)
{
cout<<it<<" ";
}
return 0;
}
2.选择排序(从小到大)
#include <iostream>
#include <vector>
using namespace std;
//选择排序
vector<int> MySort(vector<int>& arr) {
int n = arr.size();
for(int i = 0; i< n-1;i++)
{
//只有这个是需要改变的
int min_idx = i;
for(int j = i+1 ; j < n; j++)//找到[i,n-1]范围内,最小数的下标
{
if(arr[j] <arr[min_idx])min_idx = j;
}
int t = arr[i];
arr[i] = arr[min_idx];
arr[min_idx] = t;
}
return arr;
}
int main()
{
vector<int> arr{5,2,3,1,4};
for(auto it : arr)
{
cout<<it<<" ";
}
cout<<" "<<endl;
MySort(arr);
for(auto it : arr)
{
cout<<it<<" ";
}
return 0;
}
3.插入排序
#include <iostream>
#include <vector>
using namespace std;
//插入排序
/**
* 将数组分为已排序和未排序的两部分,每次从未排序中选取一个元素,将他插入到已排序的的部分的正确位置
*/
vector<int> MySort(vector<int>& arr) {
int n = arr.size();
//arr[0]是已排好序的
for(int i = 1; i < n; i++)
{
int key = arr[i];//我们要排序的元素
int j = i-1;//已排好序的部分是[0,j]
while(j >= 0 &&arr[j]>key)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;//j有可能<0,这么看来+1也就记住了吧
}
return arr;
}
int main()
{
vector<int> arr{5,2,3,1,4};
for(auto it : arr)
{
cout<<it<<" ";
}
cout<<" "<<endl;
MySort(arr);
for(auto it : arr)
{
cout<<it<<" ";
}
return 0;
}
4.归并排序
#include <iostream>
#include <vector>
using namespace std;
//归并排序
vector<int> tmp;
void merge_sort(vector<int>&q ,int l,int r)
{
if(l >= r) return;
int mid = (l + r) >>1;
merge_sort(q, l, mid);
merge_sort(q, mid+1, r);
int k = 0;//临时数组的下标
int i = l , j = mid + 1;//i<=mid < mid+1<=r/////////////
while(i <= mid && j <= r)//////////////
{
if(q[i] <= q[j])tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
while(i<=mid){tmp[k++] = q[i++];}
while(j<=r){tmp[k++] = q[j++];}
for( i = l ,j = 0 ; i <= r ; i++,j++)q[i] = tmp[j];
}
vector<int> MySort(vector<int>& arr) {
int n = arr.size();
tmp.resize(n,0);//初始化为n个元素且都为0
merge_sort(arr, 0, n-1);//0,n-1是下标
return arr;
}
int main()
{
vector<int> arr{5,2,3,1,4};
for(auto it : arr)
{
cout<<it<<" ";
}
cout<<" "<<endl;
MySort(arr);
for(auto it : arr)
{
cout<<it<<" ";
}
return 0;
}
5.快速排序
//快速排序
void quick_sort(vector<int>&q,int l ,int r)
{
if(l >= r)return;
int x = q[(l+r)>>1], i=l-1 , j=r+1;//x是最中间的那个数,i要多往前走一步,j要多往后走1步
while (i < j) {
do i++ ; while(q[i] < x);
do j-- ; while(q[j] > x);
if(i<j) swap(q[i],q[j]);//快速排序比的是下标
}
quick_sort(q, l, j);
quick_sort(q, j+1, r);
}
vector<int> MySort(vector<int>& arr) {
int n = arr.size();
quick_sort(arr,0,n-1);
return arr;
}
6.希尔排序(了解)
希尔排序是插入排序的一种优化,
他的核心思想是假定原数组中间间隔着特定的增量,然后通过对组内的元素进行插入排序,
不断缩小增量序列,从而达到有序的状态.
我只了解过基本的原理,并没有实际使用过.
7.堆排序(了解)
堆排序是基于二叉堆数据结构的一种比较排序算法。二叉堆是一种完全二叉树,其中每个父节点的值都大于或等于(小于或等于)其子节点的值,称为最大堆(最小堆)。
堆排序算法的基本思想是将待排序的数组构造成一个最大堆,然后不断调整堆,进行下沉操作,直到数组有序。
堆排序的优势在于其时间复杂度稳定为O(nlogn),不受输入数据的影响。而且不需要额外的存储空间。
这个我也只是了解过基本的原理,并没有实际使用过.
反转链表
class Solution {
public:
// ListNode* reverseList(ListNode* head) {
// if(!head)return NULL;
// auto a = head,b = head->next;
// while(b)
// {
// auto c = b->next;
// b->next= a;
// a = b;
// b = c;
// }
// head->next = NULL;
// return a;
// }
ListNode * reverseList(ListNode * head)
{
if(!head || !head->next)return head;
auto tail = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return tail;
}
};
层序遍历
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>>res;
if(!root)return res;
queue<TreeNode*>q;//中间变量
q.push(root);
while(!q.empty())
{
vector<int> level;//每一层的结点(要放到答案res里面的)
int len = q.size();//这一层的节点个数
while(len --)
{
auto t = q.front();
q.pop();
level.push_back(t->val);
//未下一层做准备
if(t->left)q.push(t->left);
if(t->right)q.push(t->right);
}
res.push_back(level);
}
return res;
}
};
#include <iostream>
#include <vector>
using namespace std;
// 提问1:指针怎么调用函数?
// 你可以使用using根据函数签名来创建一个函数指针类型
void func(int t)
{
cout << t << endl;
}
using FuncPtr = void (*)(int);
using SortPtr = void (*)(vector<int> &);
// 提问2:冒泡排序的原理是什么? 他的时间复杂度是多少?O(n^2)
void sort_1(vector<int> &arr)
{
int n = arr.size();
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
if (arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
}
}
// 提问3:选择排序的原理是什么? 他的时间复杂度是多少?O(n^2)
// 也是遍历n-1轮,他是从i为0的元素开始,直到我们将他放到合适的位置
// 选择排序的难点:最小元素的下标
// 选第1小的元素的下标,选第2小的元素的下标,选第3小的元素的下标...
void sort_2(vector<int> &arr)
{
int n = arr.size();
for (int i = 0; i < n - 1; i++)
{
int min_idx = i;
int j = min_idx + 1;
while (j < n)
{
if (arr[j] < arr[min_idx])
min_idx = j;
j++;
}
swap(arr[i], arr[min_idx]);
}
}
// 提问4:插入排序的原理是什么? 他的时间复杂度是多少?O(n^2)
// 两部分:一部分已经排好了,另一部分没排列好,我们就不断把没排好的元素插入到排好的一部分中
// 我们先把要插入元素提起来,也就是说这个元素的位置就空了,然后不断的将前面的元素往后移
void sort_3(vector<int> &arr)
{
int n = arr.size();
// 这是没排好的部分
for (int i = 1; i < n; i++)
{
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) // 前一数比这个数大了,我们就要把他后移
{
arr[j + 1] = arr[j]; // j+1这个位置被空出来了
j--;
}
swap(key, arr[j + 1]);//或者这arr[j+1]=key;也行
}
}
// 提问5:归并排序的原理是什么? 他的时间复杂度是多少?O(n log n)
// 合并两个子数组的复杂度为 O(n)),而分割的层数是对数级别的(每分割一次,数组的大小减半,
// 所以需要 log n 层分割才能到达单个元素)。
// 线性的合并复杂度乘以对数级别的层数,最终时间复杂度就是 O(n log n)
vector<int> tmp;
void merge_sort(vector<int> &q, int l, int r)
{
if (l >= r)
return;
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
int k = 0;
int i = l, j = mid + 1;
while (i <= mid && j <= r) // 想一下:i有没有可能等于mid,j有没有可能等于r
{
if (q[i] <= q[j])
tmp[k++] = q[i++];
else
tmp[k++] = q[j++];
}
while (i <= mid)
tmp[k++] = q[i++];
while (j <= r)
tmp[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++) //
q[i] = tmp[j];
}
void sort_4(vector<int> &arr)
{
int n = arr.size();
tmp.resize(n, 0);
merge_sort(arr, 0, n - 1);
}
// 提问6:快速排序的原理是什么? 他的时间复杂度是多少?平均情况下为O(n log n),最坏情况下为O(n^2)
void sort_5(vector<int> &q, int l, int r)
{
if (l >= r)
return; // 左和右是一个数,就没必要继续了(这里加等号,表示两个数相等了,那就是没必要继续了)
int x = q[l + r >> 1], i = l - 1, j = r + 1;
while (i < j) // 这里不加等号是因为:这个是只要在i不等j的情况下,就继续遍历
{
do
i++;
while (q[i] < x); // 我们要的是一个从小到到的排列顺序,所以,正常情况下是q[i]<x<q[j],直到不满足的时候,我们就把两个数进行交换
do
j--;
while (q[j] > x);
if (i < j) // 这个表示,如果i不等于j
swap(q[i], q[j]);
}
// 此刻,q[l,j]都是<=x,q[j,r]都是>=x
sort_5(q, l, j);
sort_5(q, j + 1, r);
}
// 提问7:希尔排序 插入排序Ultra
// 提问8:堆排序 O(nlogn)
int main()
{
FuncPtr ptr = func;
ptr(2);
func(1);
printf("你好\n");
vector<int> array{11, 412, 41, 454, 1, 2, 4545, 24, 4574};
cout << "排序前:";
for (auto x : array)
{
cout << x << ' ';
};
// SortPtr ptr1 = sort_3;
// ptr1(array);
// using SortPtrUltr = void (*)(vector<int> &, int, int);
// SortPtrUltr ptr2 = sort_5;
// ptr2(array, 0, array.size() - 1);
using Sort_merge = void (*)(vector<int> &);
Sort_merge ptr3 = sort_4;
ptr3(array);
cout << endl
<< "排序后:";
for (auto x : array)
{
cout << x << ' ';
};
return 0;
}
总结一下:
O(n^2)就是两层循环:for+for,或者for+while
- 冒泡排序:O(n^2),第一次将第一大的浮出水面,第二次将第二大的浮出水面,...
- 选择排序:O(n^2),第一次拿到第一小元素的下标,第二次拿到第二小元素下标...
- 插入排序:O(n^2),将未排好顺序的部分,一个元素一个元素的插入到排好顺序的部分,
比如举个例子:将x插入到[0,j]的部分,每次在遇到x<q[j]时,q就往后移动一位,直到x不再小于为止,那个位置就是x应该插入的位置
-
快速排序:平均情况下为O(n log n),最坏情况下为O(n^2),==先治后分==,取一个标准,比如说中间值,我设置为x,不断将数组分为<=x的部分,和>=x的部分,双指针从两边走,走不动时(不满足q[i]<x<q[j]),就交换
-
归并排序:O(n log n),分治思想,==先分后治==,分成[l,mid]和[mid+1,r],
,看成两个数组,每次取每个数组的最小值,加入到临时数组中,
最后在把临时数组放到最终的数组中(临时数组每次递归都是从下标0开始的)