+++ author = "Wxn" title = "2024-04-20七大排序算法+层序遍历" date = "2024-04-20" description = "Please read me first." tags = [ "Dilay", ] categories = [ "面试复盘", ]

+++

This article offers a sample of basic Markdown.

正文开始

https://www.nowcoder.com/login?callBack=%2Fprofile%2F319706329%2FcodeBookDetail%3FsubmissionId%3D416948138

1.冒泡排序(从小到大)

#include <iostream>
#include <vector>

using namespace std;

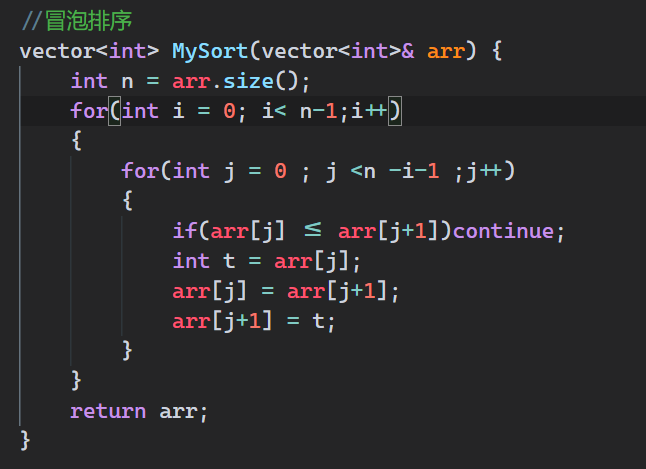
//冒泡排序
vector<int> MySort(vector<int>& arr) {
    int n = arr.size();
    for(int i = 0; i< n-1;i++)//冒泡排序和选择排序都是0~n-1轮
    {
        for(int j = 0 ; j <n -i-1 ;j++)
        {
            if(arr[j] <= arr[j+1])continue;
            int t = arr[j];
            arr[j] = arr[j+1];
            arr[j+1] = t;
        }
    }
    return arr;
}

int main()
{
    vector<int> arr{5,2,3,1,4};
    for(auto it : arr)
    {
        cout<<it<<" ";
    }
    cout<<" "<<endl;
    MySort(arr);
    for(auto it : arr)
    {
        cout<<it<<" ";
    }
    return 0;
}

2.选择排序(从小到大)

#include <iostream>
#include <vector>

using namespace std;

//选择排序
vector<int> MySort(vector<int>& arr) {
    int n = arr.size();
    for(int i = 0; i< n-1;i++)
    {
        //只有这个是需要改变的
        int min_idx = i;
        for(int j = i+1 ; j < n; j++)//找到[i,n-1]范围内,最小数的下标
        {
            if(arr[j] <arr[min_idx])min_idx = j;
        }
        int t = arr[i];
        arr[i] = arr[min_idx];
        arr[min_idx] = t;
    }
    return arr;
}

int main()
{
    vector<int> arr{5,2,3,1,4};
    for(auto it : arr)
    {
        cout<<it<<" ";
    }
    cout<<" "<<endl;
    MySort(arr);
    for(auto it : arr)
    {
        cout<<it<<" ";
    }
    return 0;
}

3.插入排序

#include <iostream>
#include <vector>

using namespace std;

//插入排序
/**
* 将数组分为已排序和未排序的两部分,每次从未排序中选取一个元素,将他插入到已排序的的部分的正确位置
*/
vector<int> MySort(vector<int>& arr) {
    int n = arr.size();
    //arr[0]是已排好序的
    for(int i = 1; i < n; i++)
    {
        int key = arr[i];//我们要排序的元素
        int j = i-1;//已排好序的部分是[0,j]
        while(j >= 0 &&arr[j]>key)
        {
            arr[j+1] = arr[j];
            j--;
        }
        arr[j+1] = key;//j有可能<0,这么看来+1也就记住了吧
    }
    return arr;
}

int main()
{
    vector<int> arr{5,2,3,1,4};
    for(auto it : arr)
    {
        cout<<it<<" ";
    }
    cout<<" "<<endl;
    MySort(arr);
    for(auto it : arr)
    {
        cout<<it<<" ";
    }
    return 0;
}

4.归并排序

#include <iostream>
#include <vector>

using namespace std;

//归并排序
vector<int> tmp;
void merge_sort(vector<int>&q ,int l,int r)
{
    if(l >= r) return;

    int mid = (l + r) >>1;
    merge_sort(q, l, mid);
    merge_sort(q, mid+1, r);

    int k = 0;//临时数组的下标
    int i = l , j = mid + 1;//i<=mid < mid+1<=r/////////////
    while(i <= mid && j <= r)//////////////
    {
        if(q[i] <= q[j])tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    }

    while(i<=mid){tmp[k++] = q[i++];}
    while(j<=r){tmp[k++] = q[j++];}
    for( i = l ,j = 0 ; i <= r ; i++,j++)q[i] = tmp[j];
}
vector<int> MySort(vector<int>& arr) {
    int n = arr.size();
    tmp.resize(n,0);//初始化为n个元素且都为0
    merge_sort(arr, 0, n-1);//0,n-1是下标
    return arr;
}
int main()
{
    vector<int> arr{5,2,3,1,4};
    for(auto it : arr)
    {
        cout<<it<<" ";
    }
    cout<<" "<<endl;
    MySort(arr);
    for(auto it : arr)
    {
        cout<<it<<" ";
    }
    return 0;
}

5.快速排序

//快速排序
void quick_sort(vector<int>&q,int l ,int r)
{
    if(l >= r)return;
    int x = q[(l+r)>>1], i=l-1 , j=r+1;//x是最中间的那个数,i要多往前走一步,j要多往后走1步
    while (i < j) {
        do i++ ; while(q[i] < x);
        do j-- ; while(q[j] > x);
        if(i<j) swap(q[i],q[j]);//快速排序比的是下标
    }
    quick_sort(q, l, j);
    quick_sort(q, j+1, r);
}
vector<int> MySort(vector<int>& arr) {
    int n = arr.size();
    quick_sort(arr,0,n-1);
    return arr;
}

6.希尔排序(了解)

希尔排序是插入排序的一种优化,

他的核心思想是假定原数组中间间隔着特定的增量,然后通过对组内的元素进行插入排序,

不断缩小增量序列,从而达到有序的状态.

我只了解过基本的原理,并没有实际使用过.

7.堆排序(了解)

堆排序是基于二叉堆数据结构的一种比较排序算法。二叉堆是一种完全二叉树，其中每个父节点的值都大于或等于（小于或等于）其子节点的值，称为最大堆（最小堆）。

堆排序算法的基本思想是将待排序的数组构造成一个最大堆，然后不断调整堆,进行下沉操作，直到数组有序。

堆排序的优势在于其时间复杂度稳定为O(nlogn)，不受输入数据的影响。而且不需要额外的存储空间。

这个我也只是了解过基本的原理,并没有实际使用过.